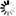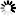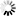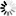The CSQRT function accepts a complex number and returns the complex square root of that number. The complex square root of a number is calculated first by means of DeMoivre's relationship and then taking its square root, as follows:

CSQRT(z)=(r)**1 /2(COS(phi/2) + i SIN(phi/2))  

Using the half-angle formulas for the cosine and sine and rearranging the preceding relationship, the following equation is derived:

CSQRT(z)=SQRT(r(1+COS(phi))/2)+(SQRT(r(1-COS(phi))/2)*i)  

The identity x/r=COS(phi) and algebraic manipulation result in the algorithm that is used.

If x >= 0 and r = CABS(x+iy), then

CSQRT(x+iy)=SQRT((r+x)/2)+iy/(2 SQRT((r+x)/2))   

If x < 0, then the trigonometric functions in polar form are complemented, and the following algorithm results, where r = CABS (x+iy):

(SQRT(x+iy)=y/(2*SQRT((t+ABS(x))/2))+ i SIGN(y)*SQRT((r+ABS(x))/2)  

SIGN(y) is a function that has the value +1 if y is not negative and the value -1 otherwise.