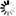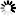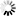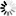The CSIN function accepts a complex number and returns the sine of that number. The sine of a complex number z is calculated by the use of the identity for SIN(a+b) on the complex number x+iy. Then the identities COS(iy) = COSH(y) and SIN(iy) = SINH(y) are applied. Refer to the definitions under “Definitions Used in Complex Function Descriptions” earlier in this section. When the definitions of the hyperbolic sine and cosine are substituted in the equation, the algorithm is as follows:

CSIN(x+iy) = (+or-)1/2*SQRT(1-COS**2 (x))*(e**y+e**(-y))
+i/2 COS(x)*(e**y-e**(-y))  

The value of x is taken modulo 2pi before the COS function is applied. The negative sign is applied on the square root if the original x was in the third or fourth quadrant.