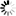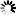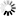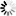All the complex functions are derived by the use of the real functions. In these functions, several methods are used to write a complex number. When a complex number is described as a simple variable, the letter z is used. Several equivalent ways of writing z exist. In the following example, x and y are real numbers and i equals SQRT(-1):

z = x + iy

The variable z can also be expressed as follows:

z=re**(i*phi)

The variables r and phi are the absolute value and the displacement, respectively. They are related to x and y as follows:

x = r COS(phi)
y = r SIN(phi)
r**2 = x**2 + y**2
TAN(phi) = x/y 

These identities also indicate DeMoivre's formula as follows:

e**(i*phi) = COS(phi) + iSIN(phi) 

These basic relationships are used to determine most of the complex algorithms.